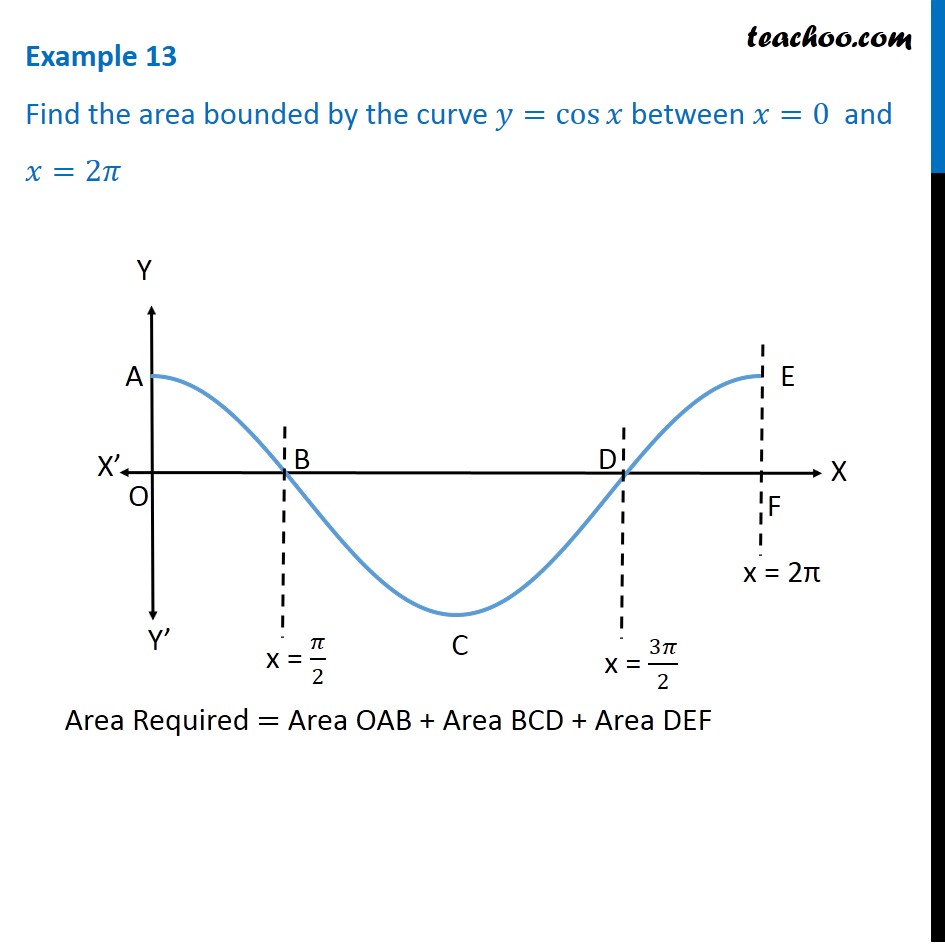
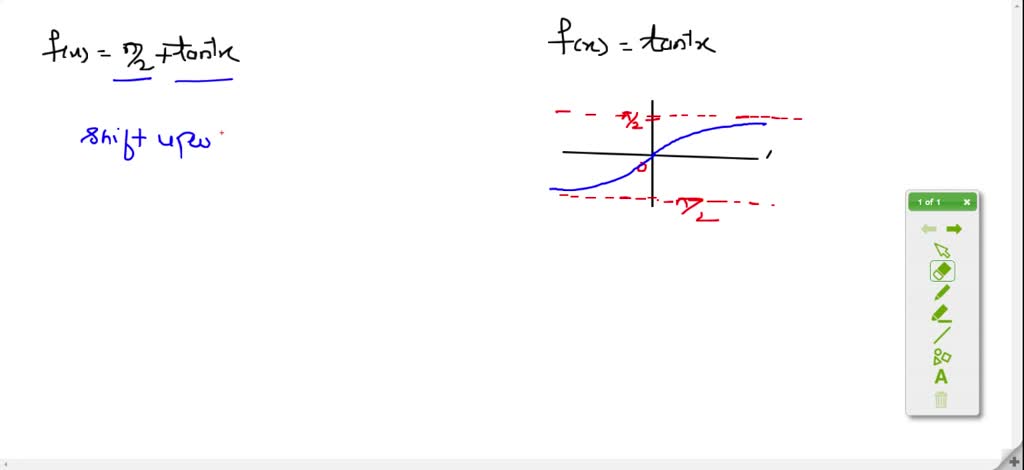
So why of minus X equals going to be equal to Y Of X And so you can see the symmetry about, okay um when X equals zero of clearly um Y is zero
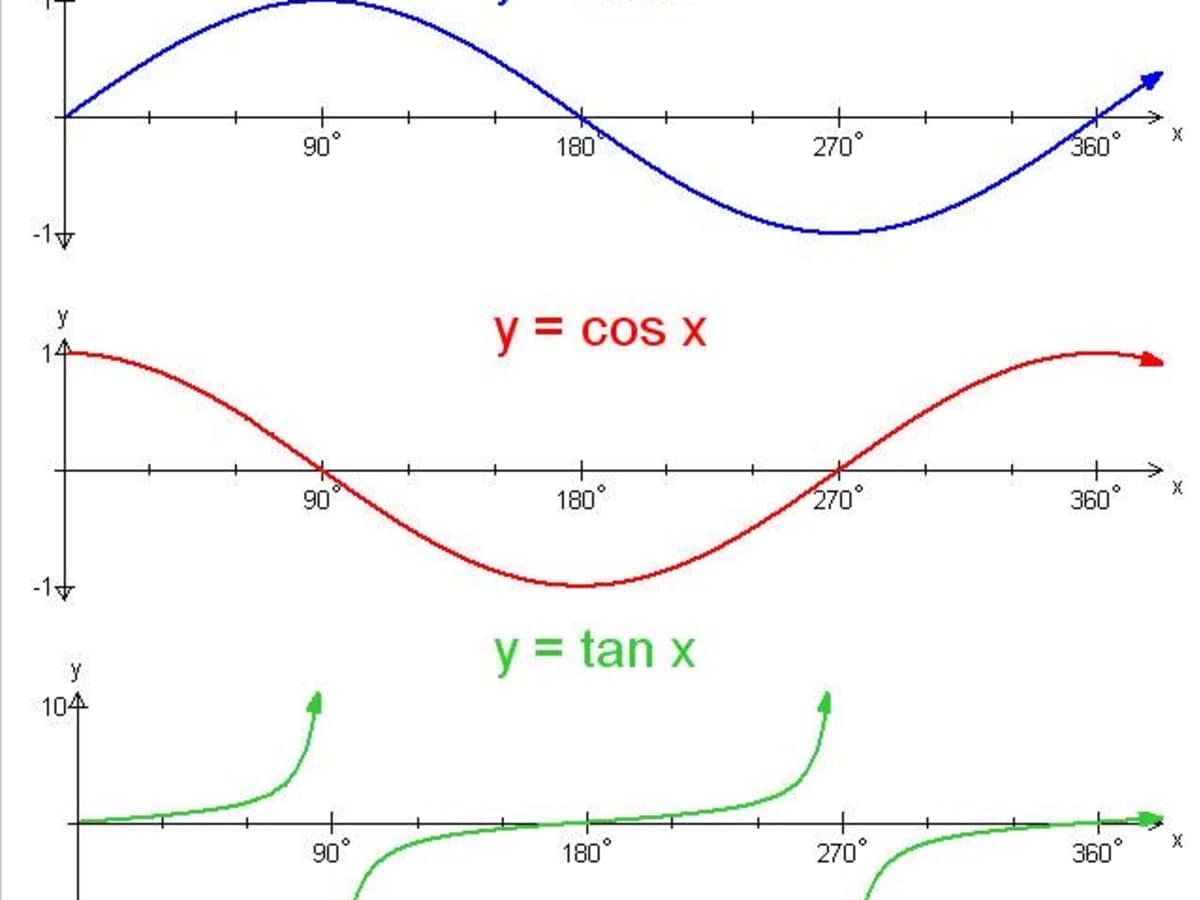
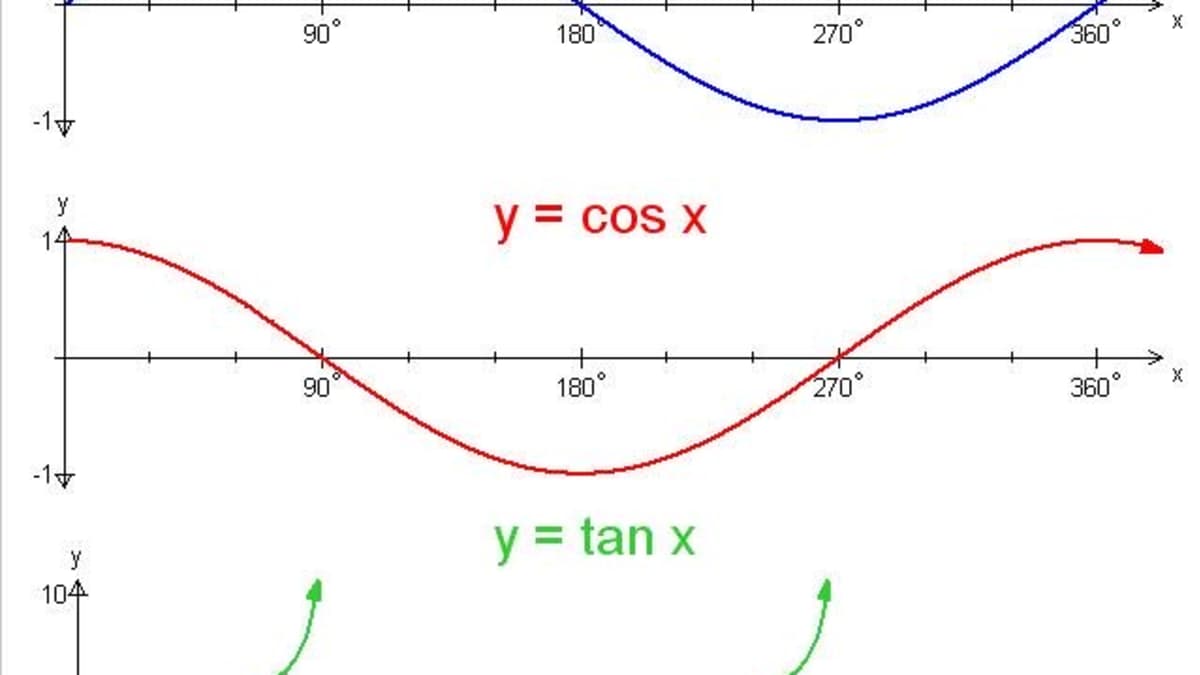
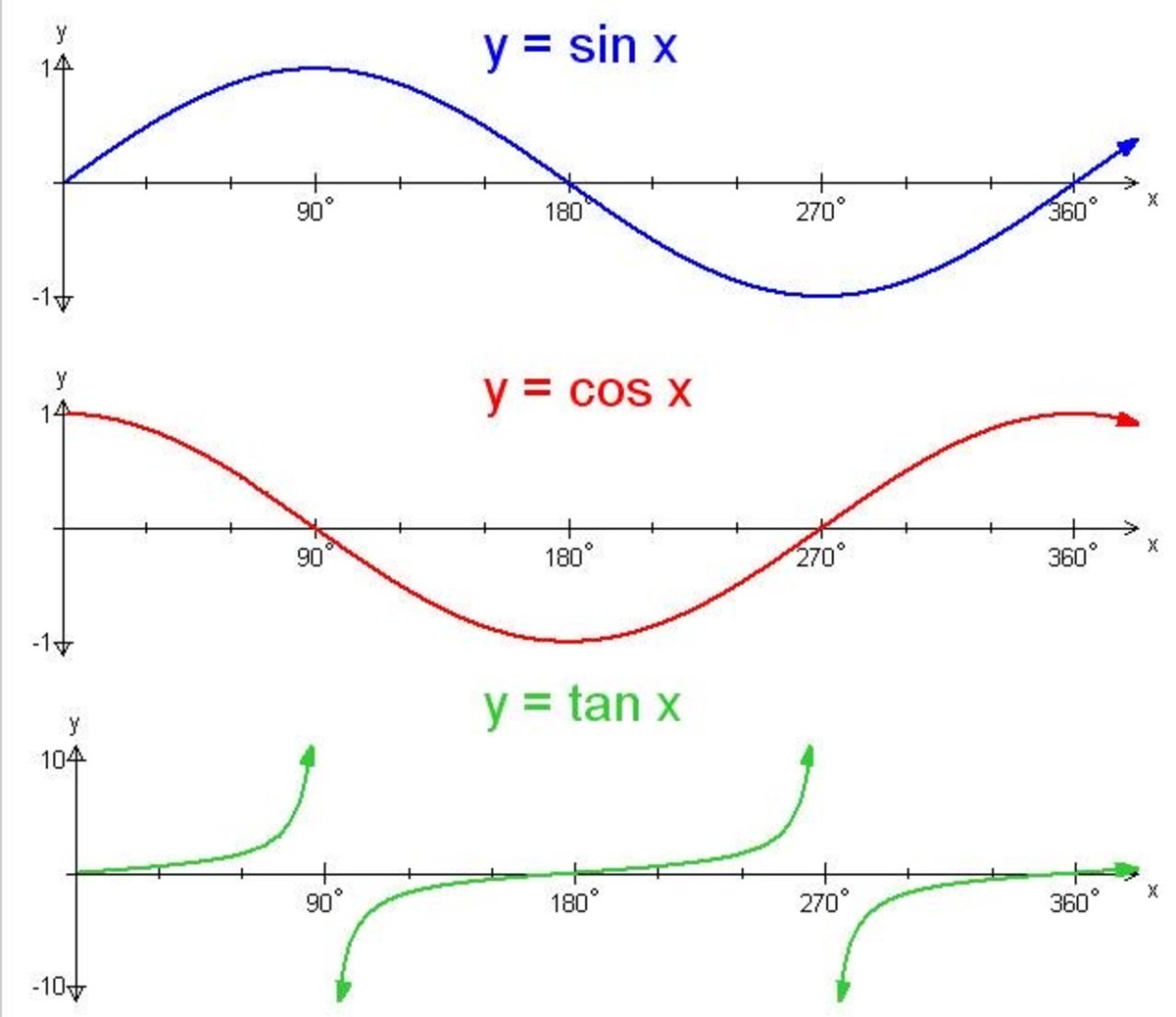
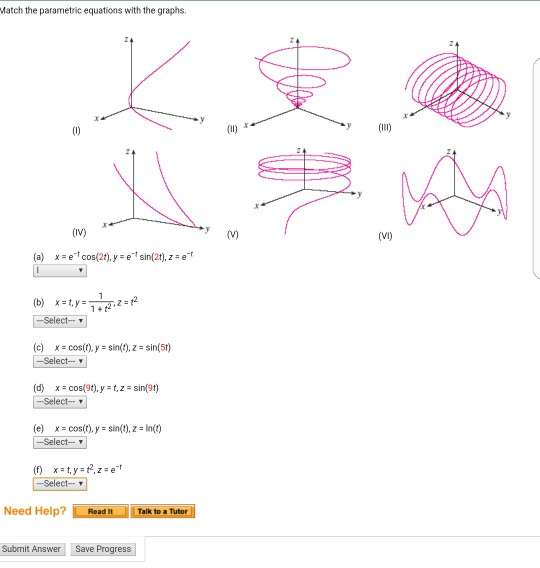
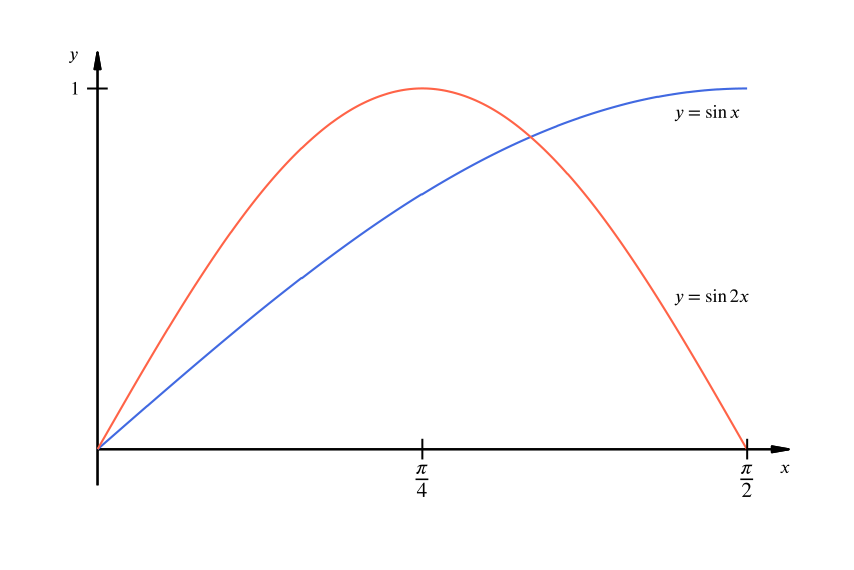
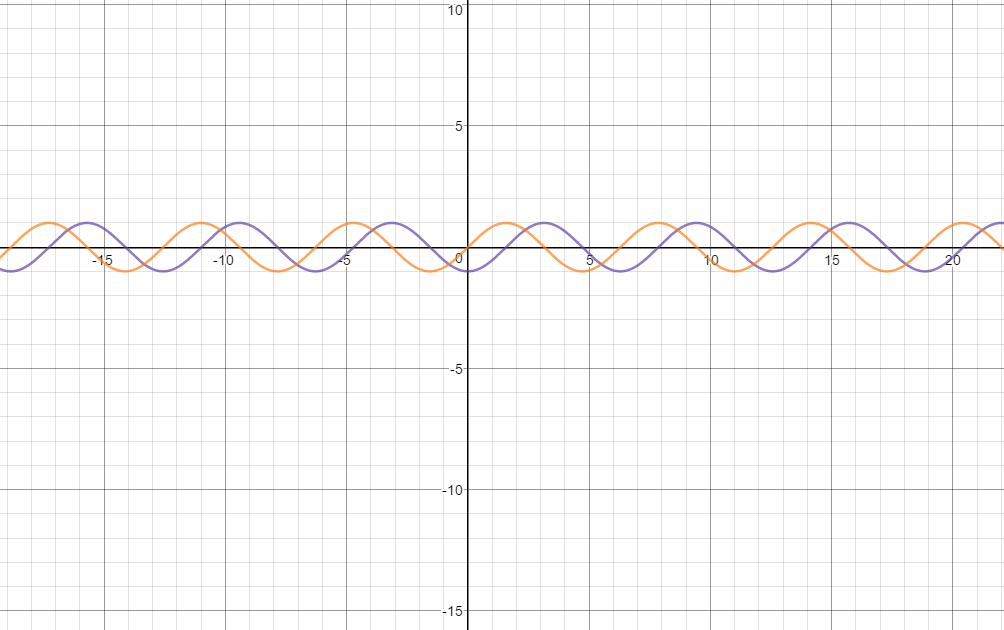
Y=sin^2(x)+cos^2(x) graph- Cos (2x) and sin (2x) have periods of pi, compared to a period of 2pi for cos (x) and sin (x)the graphs are still identical but in this case the lateral shift is pi 4so make a left shift (on the graph of sin (2x)) or a right shift (on the graph of cos (2x)) by pi 4 units, and you will see that the graphs coincide Answer steps to solve to graph y = cos(x), we need to be familiar with theLearn how to graph y=cos(xπ/6) using transformations NOTE graphs are not drawn to scale Please make sure to plot your points for accuracy
Y=sin^2(x)+cos^2(x) graphのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
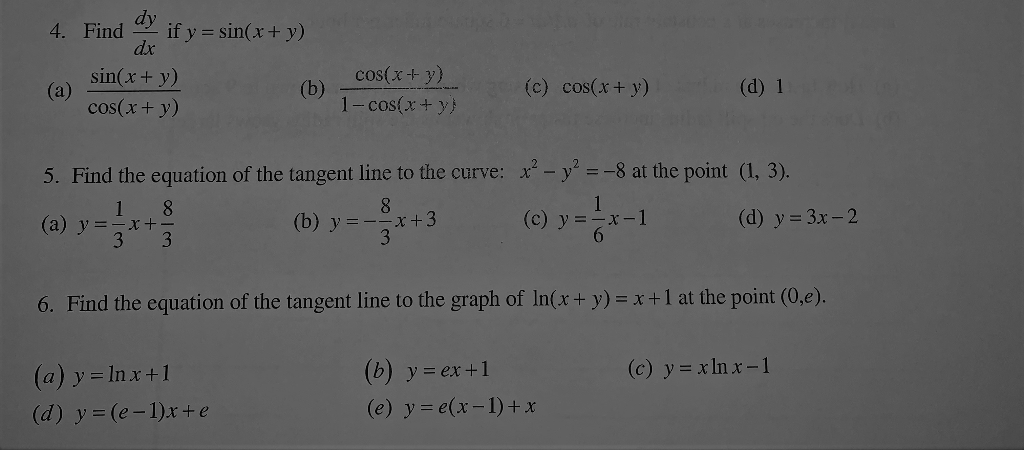 |  | |
 |  | |
 |  | |
「Y=sin^2(x)+cos^2(x) graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 |  | |
「Y=sin^2(x)+cos^2(x) graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 |  | |
「Y=sin^2(x)+cos^2(x) graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「Y=sin^2(x)+cos^2(x) graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「Y=sin^2(x)+cos^2(x) graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「Y=sin^2(x)+cos^2(x) graph」の画像ギャラリー、詳細は各画像をクリックしてください。
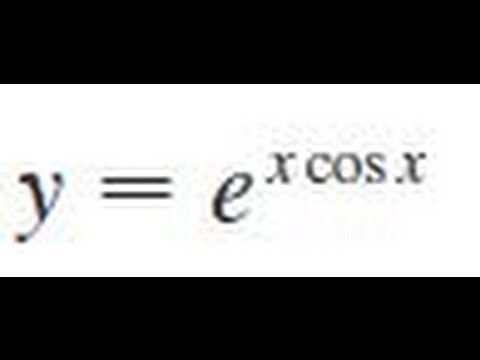 |  | |
 |  | |
「Y=sin^2(x)+cos^2(x) graph」の画像ギャラリー、詳細は各画像をクリックしてください。
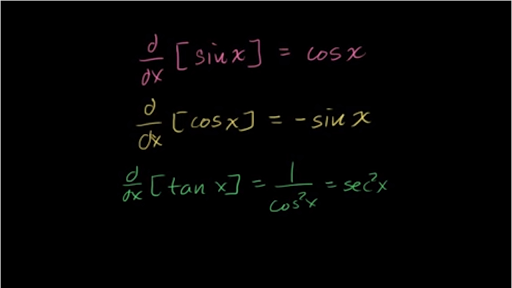 |  | |
 | ||
 |  | |
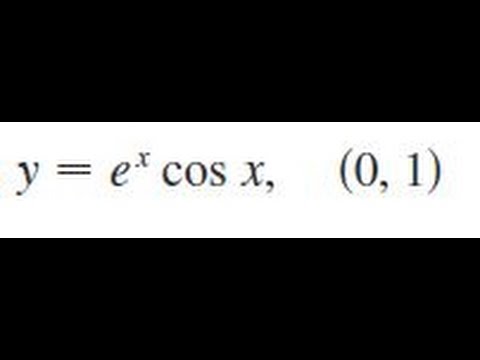 |  | |
「Y=sin^2(x)+cos^2(x) graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |
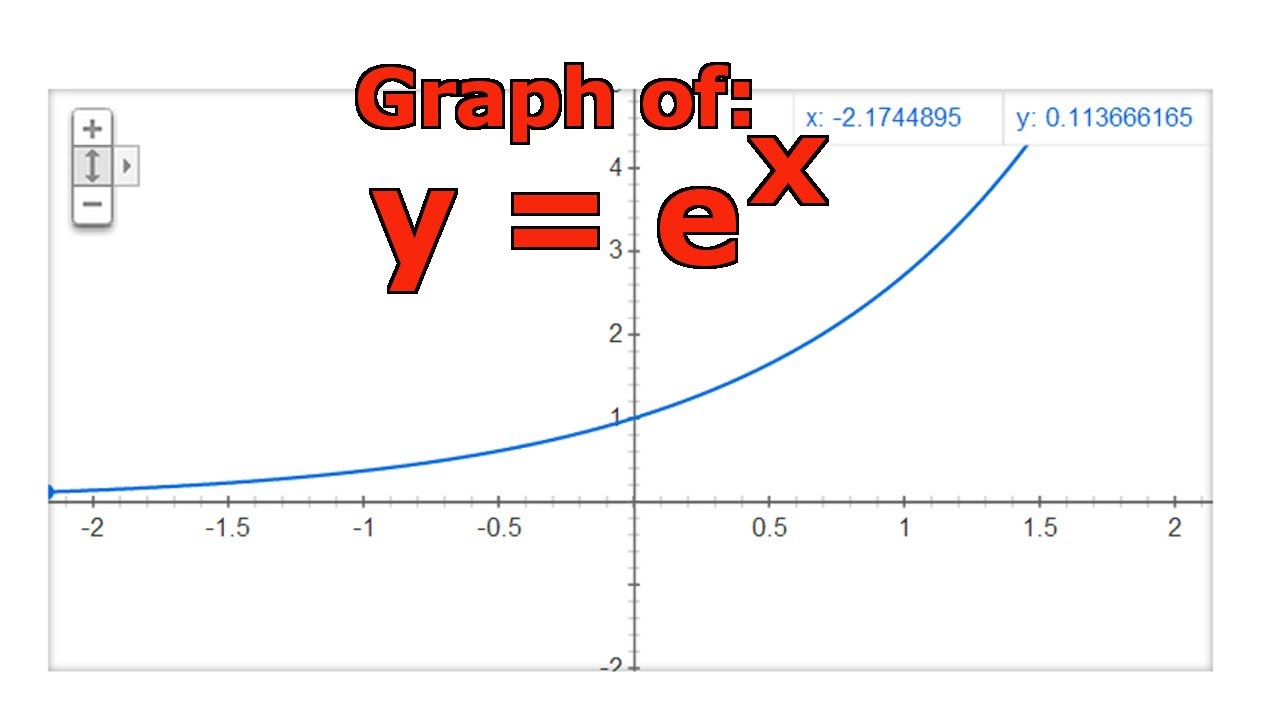
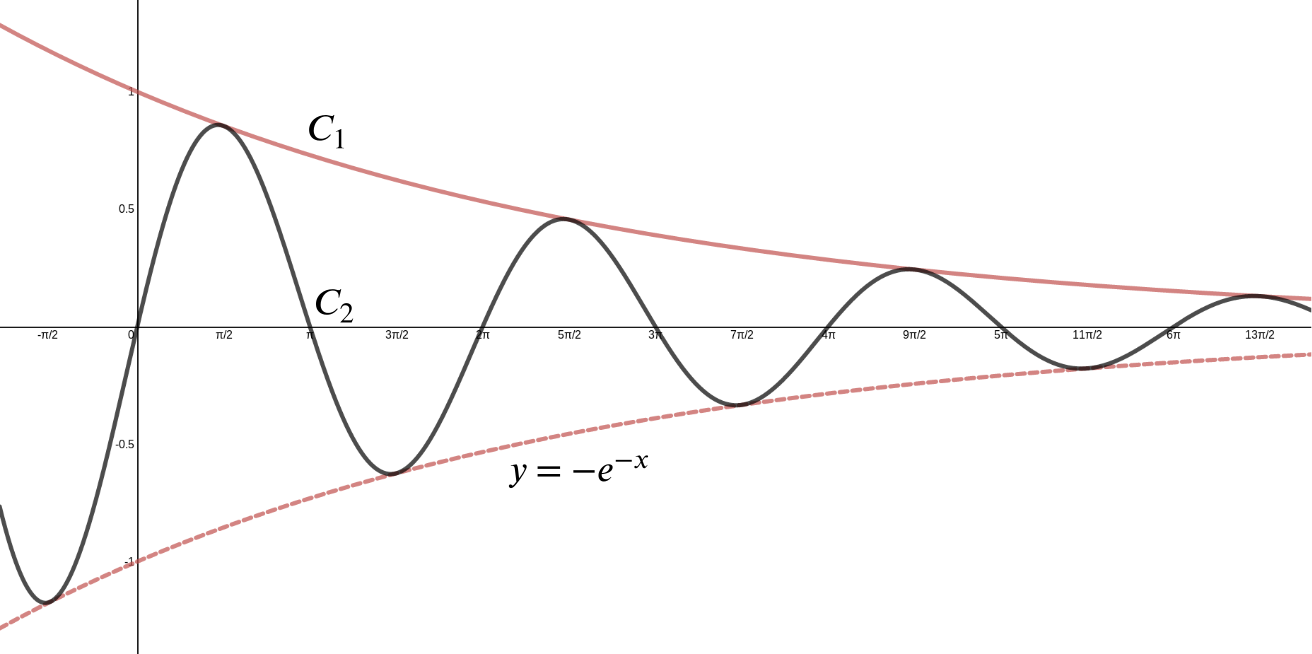
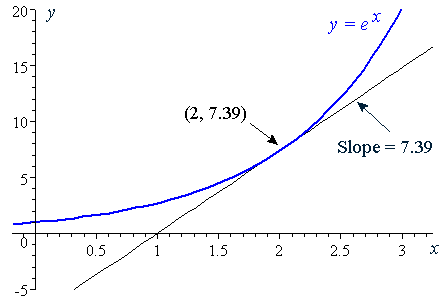
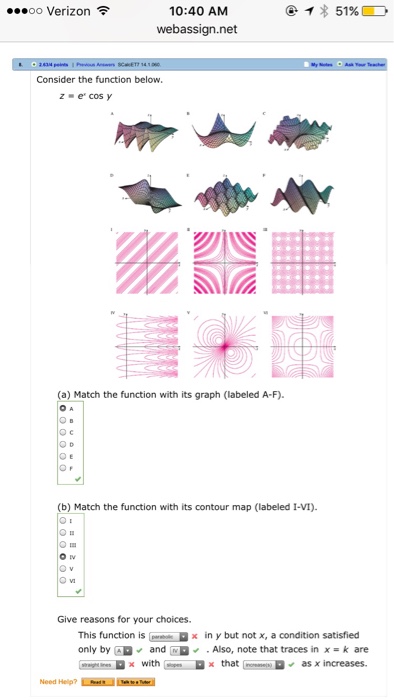
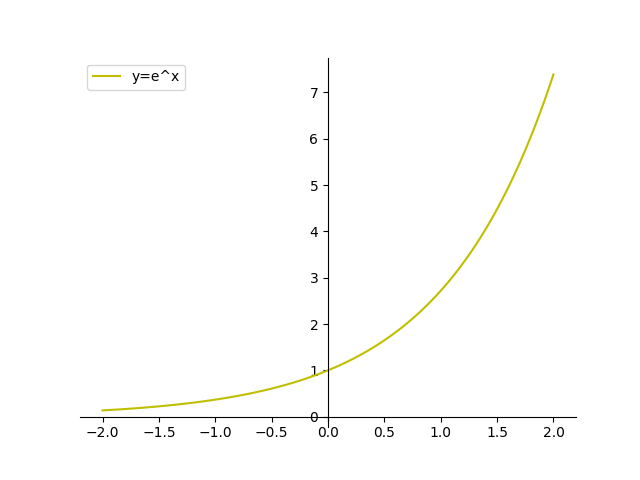
This is a type of problem involving the product rule The product rule states d/dxf(x) * g(x) = f'(x)g(x) f(x)g'(x) So, we will let f(x) = e^x, and g(x) = cos x We know that the derivative of e^x is simply e^x, and that the derivative of cos x is equal to sin x (if these identities look unfamiliar to you, I may recommend viewing videos from this page or this page, which explain theGraph y=e^ (x) y = e−x y = e x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0
Incoming Term: y 2 cos x graph, y=sin^2(x)+cos^2(x) graph, y 3 cos x graph, y=4 cos x graph,



